Time to Consider LEAPS
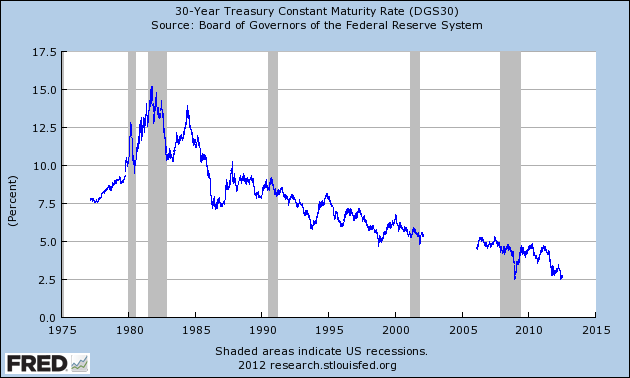
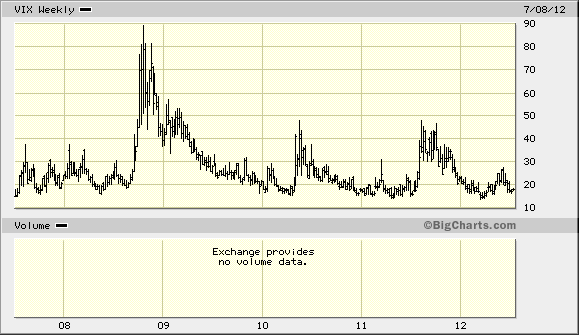 Low interest rates and low volatility mean LEAPs MAY be a cheap, non-recourse loan for owning a growing business or a way to lower your over-all exposure without giving up returns.
Low interest rates and low volatility mean LEAPs MAY be a cheap, non-recourse loan for owning a growing business or a way to lower your over-all exposure without giving up returns.
Rising interest rates and volatility (all else being equal) will raise the price of your leap. If you believe a company will grow its intrinsic value 10% to 15% in the next 18 months to two years then leaps may be an attractive tool. Option traders’ models do not do as well as the cone of uncertainty increases (the time period until expiration is beyond a year).
A refresher on options:Options_Guide but the Bible on options is Options As a Strategic Investment by Lawrence G. McMillan. See Chapter 25, Leaps.
Lecture by a Great Value Investor on using Leaps: Lecture-8-on-LEAPS A MUST READ.
Application of Leaps
This blog discusses using Leaps for Cisco during 2011. http://www.valuewalk.com/2011/07/cisco-leaps-opportunity-lifetime/
I am not recommending that you agree, but follow the logic.
If you are new to investing then stay away, but for some, NOW may be a time to use this tool with the right company at the right price.
Good luck and be careful not to over-use options. Options, when you are successful, can become as addictive as crack–who doesn’t like making 10 times your money?



14 responses to “Leaps-Perhaps Time to Pull Out Another Tool from Your Arsenal.”